台灣市場常見連動債類型(二)連結數檔股票ELN的賽局分析(1)

為了進一步說明ELN的賽局(Game Theory)分析，我們要先談一般權益證券價格（或指數）的走勢分佈。

在連動債DIY--如何架構高收益型連動債（ELN）中，眼尖的讀者，會發現其中的兩張圖，有一點玄機：

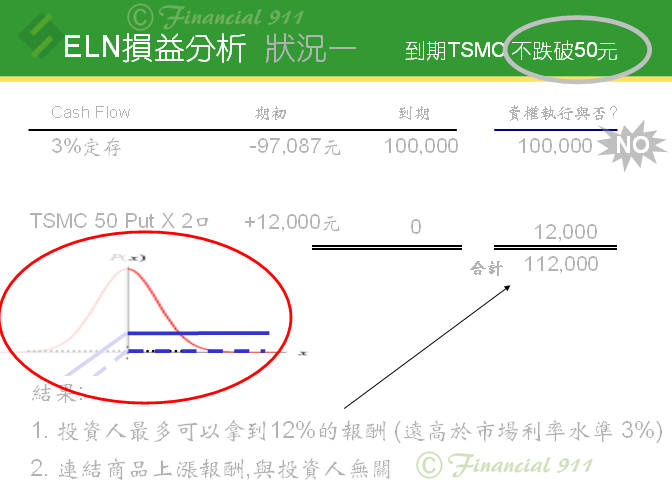
紅色圈圈內，那個紅色曲線是什麼意思？為什麼出現在這裏？

如果股價遵行隨機漫步理論，未來股價則呈現如下圖的分佈：

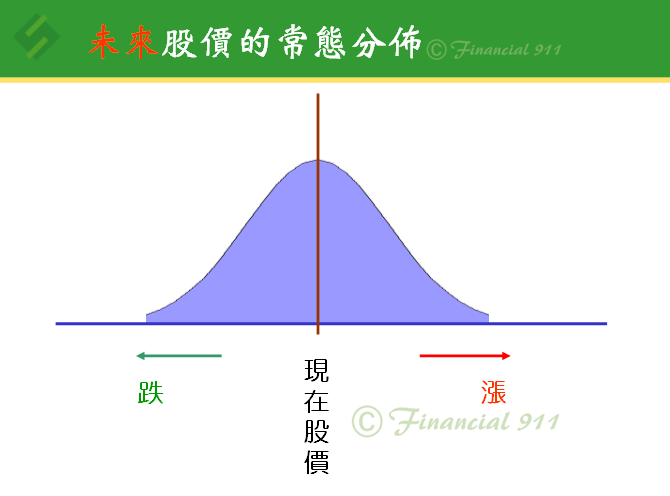
意思就是，未來股價，漲、跌的機會各半，而且，隨著漲（跌）幅的拉大，其可能性（發生的次數）將越小。

也許有人在質疑股價是否真的會遵守隨機漫步，那麼，我們來看一下台灣加權指數的分佈*：

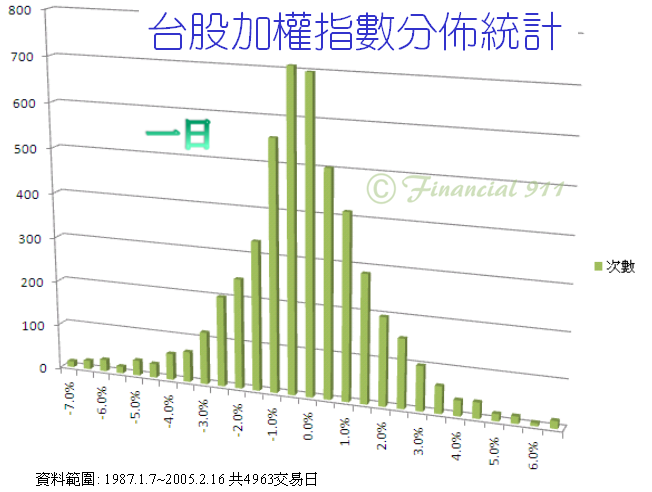
由上圖可以看出，大致上，股價或指數是遵遁隨機漫步的，當然，其些微的差異（以次數來看的話），發生在大漲、大跌的次數，比常態分佈的機會要大。這裏所指的「機會要大」，也不過是幾次而已，但若常態分佈，可能一萬次只能發生一、二次，但真實世界，則每隔二到五年就來個一次。例如：九一一恐怖攻擊、九二一大地震、三一九兩顆子彈事件..等。

但總的來說，這種極端的狀況，統計上的次數，還是較少發生，但足以讓沒有作好風險規劃的投資人，受到慘痛的教訓，甚至破產。

因為台灣有漲趺7%的限制，所以沒有一天內，超過正負7%的情況發生。但若持有加權指數五天，則分佈如下圖：

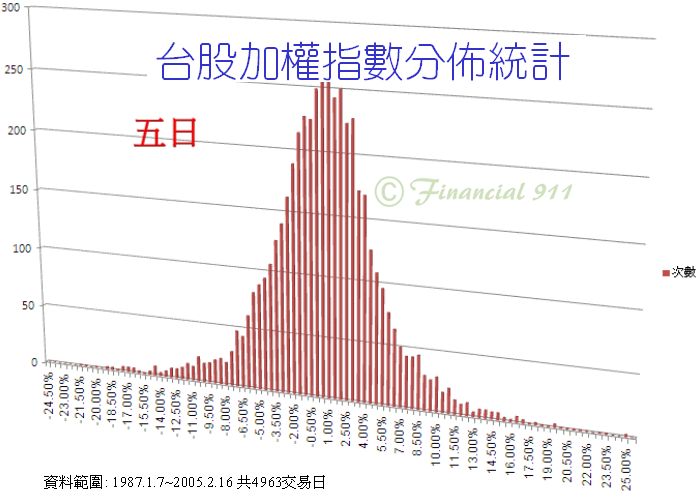
持有五日，當然就有可能漲跌超過7%，但要大盤連跌五天機會是很少很少的，甚至連三天大盤跌（漲）停，使幅度超過22%的機會，在這5千個交易日中，也是屬於少數極端的狀況。

我們將一天、五天的分佈放在一起比較：

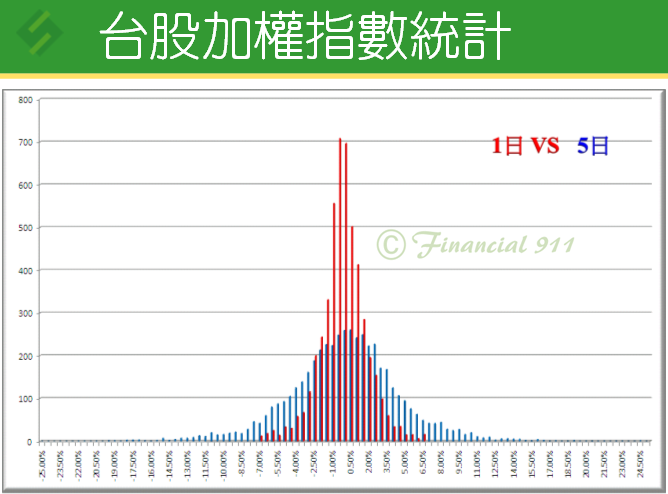
因此，我們可以了解：

• 真實世界的股價分佈，大致符合常態分佈。
• 但其極端的狀況，出現的頻率，將遠較常態分佈大的多。這些極端狀況，將讓投資人，賺到異常的利潤或造成不可彌補的重大損失。
• 當持有時間越長，分佈將越往兩側拉開（變胖、變矮）

 

*統計期間:1987/1至2005/2共五千個營業日資料。